Busy Beaver Simulations

1. Introduction

Here I present (partial) simulation results of some TMs. Such a simulation result contains a table of the transitions for the TM, and a listing of tape contents, one line for one configuration, for a few hundred initial steps. This can be of great help in getting a grasp of "what the TM does".

2. Recent Changes

• 06-Jul-2010: Added a new champion with 6 states and 2 symbols communicated by email from Pavel Kropitz (at 30-Jun-2010). It produces over 3.5x10¹⁸²⁶⁷ ones in more than 7.4x10³⁶⁵³⁴ steps.
• 05-May-2010: Added a new champion with 6 states and 2 symbols communicated by email from Pavel Kropitz (a student from prague). It produces over 3.1x10¹⁰⁵⁶⁶ ones in more than 3.8x10²¹¹³² steps. These numbers are more than 7 times as long (!) as the previous record!
• More (less recent) changes are listed near the end.

3. Simulation Styles

Currently I offer the following versions of simulation:

1. Plain: this is the simple naive way, and what you would expect a TM to do.
2. With reduced repetitions: Long repetitions of the same state reading the same tape symbol and hence doing the same action can become boring. This version omits the intermediate tapes of such a repetition.
3. With exponents: This is the equivalent 1-macro machine with the same tape symbols, and explicit tape symbol repetition counts, shown as exponents.
4. As a real macro machine: This is an equivalent macro machine, with a hand selected macro cell size, and sometimes with a hand selected amount of the original tape behind the macro head pulled into the macro state. Like all macro machines it has explicit symbol repetition counts, shown as exponents.
5. With "pure additive configuration transitions" (PA-CTRs): This machine basically operates like the macro machine above. But it remembers the configurations and recognizes when a complete configuration is repeated, except for some of the exponent values. Then it proves that step with non-negative symbolic variables in the exponents, remembers the complete "configuration transition", and later can apply it.
   The "pure additive" restricts the exponent changes to the addition of a constant value (positive or negative).
   Since the configuration does not change except for the variable exponents, the same PA-CTR can be applied again and again, until some exponent value becomes too small for the application.

With PA-CTRs the complete 5-state record list and part of the 6-state record list can be simulated and shown until the TM halts.

4. Simulation Table

An exclamation mark (!) is added to the link, where the simulation is complete (until the TM halts). An at-sign (@) is appended to the link, where the TM is shown to not halt (to loop).

Source	Plain	With repetitions reduced	With exponents	As macro machine	With PA-CTRs
From the example list in our paper	#1  #2  #3  #4  #5  #6  #7  #8	#1  #2  #3  #4  #5  #6  #7  #8	#1  #2  #3  #4  #5  #6  #7  #8	#1  #2  #3  #4  #5  #6  #7  #8	#1!  #2!  #3@  #4  #5  #6  #7!  #8@
From our 5-state record list	#1  #2  #3  #4  #5  #6  #7	#1  #2  #3  #4  #5  #6  #7	#1  #2  #3  #4  #5  #6  #7	#1  #2  #3  #4  #5  #6  #7	#1!  #2!  #3!  #4!  #5!  #6!  #7!
From our old 6-state record list	#1  #2  #3	#1  #2  #3	#1  #2  #3	#1  #2  #3	#1!  #2!  #3!
New 4-tupel 6-state record machines from Machado/Pereira	#1!	#1!	#1!	#1!	#1!
New 4-tupel 7-state record machines from Machado/Pereira	#1!  #2!  #3!	#1!  #2!  #3!	#1!  #2!  #3!	#1!  #2!  #3!	#1!  #2!  #3!
From our new 6-state record list	#a  #b  #c  #d  #e  #g  #i  #j  #k  #l  #m  #n  #o  #p  #q  #r	#a  #b  #c  #d  #e  #g  #i  #j  #k  #l  #m  #n  #o  #p  #q  #r	#a  #b  #c  #d  #e  #g  #i  #j  #k  #l  #m  #n  #o  #p  #q  #r	#a  #b  #c  #d  #e  #g  #i  #j  #k  #l  #m  #n  #o  #p  #q  #r	#a!  #b!  #c!  #d!  #e!  #g!  #i!  #j!  #k!  #l  #m  #n  #o  #p  #q  #r
3-state 3-symbol machines from Allen Brady	#SB  #b  #c  #d	#SB  #b  #c  #d	#SB  #b  #c  #d	#SB!  #b  #c  #d	#SB!  #b!  #c!  #d!
3-state 3-symbol machines from Myron Souris (email)	#a  #b	#a  #b	#a  #b	#a  #b	#a!  #b!
3-state 3-symbol machines from G. Lafitte and C. Papazian (email)	#a  #b  #c  #d  #e	#a  #b  #c  #d  #e	#a  #b  #c  #d  #e	#a  #b  #c  #d  #e	#a!  #b!  #c!  #d!  #e!
2-state 5-symbol machines from G. Lafitte and C. Papazian (email)	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j	#a!  #b!  #c!  #d!  #e!  #f!  #g!  #h!  #i!  #j
BB: 2 states (2 symbols) (cited from P. Michel)	#bb22!	#bb22!	#bb22!	#bb22!	#bb22!
BB: 3 states (2 symbols) (cited from P. Michel)	#bb32O!  #bb32S!	#bb32O!  #bb32S!	#bb32O!  #bb32S!	#bb32O!  #bb32S!	#bb32O!  #bb32S!
BB: 4 states (2 symbols) (cited from P. Michel)	#bb42!	#bb42!	#bb42!	#bb42!	#bb42!
2 states and 3 symbols (cited from P. Michel)	#a!  #b!  #cb!	#a!  #b!  #cb!	#a!  #b!  #cb!	#a!  #b!  #cb!	#a!  #b!  #cb!
2 states and 4 symbols (cited from P. Michel)	#a  #b  #c	#a  #b  #c	#a  #b  #c	#a  #b  #c	#a!  #b!  #c!
2 states and 4 symbols from T.J. & S. Ligocki	#a	#a	#a	#a	#a!
2 states and 5 symbols from T.J. & S. Ligocki	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j  #k  #l  #m  #n	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j  #k  #l  #m  #n	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j  #k  #l  #m  #n	#a  #b  #c  #d  #e  #f  #g  #h  #i  #j  #k  #l  #m  #n	#a!  #b!  #c!  #d!  #e!  #f!  #g!  #h!  #i!  #j!  #k!  #l!  #m!  #n
2 states and 6 symbols from T.J. & S. Ligocki	#a  #b  #c  #d  #e  #f  #g	#a  #b  #c  #d  #e  #f  #g	#a  #b  #c  #d  #e  #f  #g	#a  #b  #c  #d  #e  #f  #g	#a!  #b!  #c!  #d!  #e  #f  #g
3 states and 3 symbols from T.J. & S. Ligocki	#a  #b	#a  #b	#a  #b	#a  #b	#a!  #b!
3 states and 4 symbols from T.J. & S. Ligocki	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b!  #c!  #d  #e  #f  #g  #h  #i
4 states and 3 symbols from T.J. & S. Ligocki	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a  #b  #c  #d  #e  #f  #g  #h  #i	#a!  #b  #c  #d  #e  #f  #g  #h  #i
6 states and 2 symbols from T.J. & S. Ligocki	#a  #b	#a  #b	#a  #b	#a  #b	#a  #b
6 states and 2 symbols from Pavel Kropitz (full numbers)	#a  #b	#a  #b	#a  #b	#a  #b	#a  #b
Unusual symbol sizes by Marxen & Buntrock	#u9  #u13  #u80  #u154	#u9  #u13  #u80  #u154	#u9  #u13  #u80  #u154	#u9  #u13  #u80  #u154	#u9@  #u13@  #u80@  #u154@(1MB)

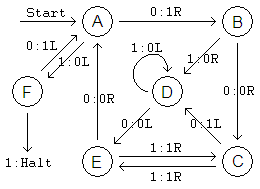
In Wikipedia I found an image of the state diagram for the #r from our new 6-state record list, the former 6-state 2-symbol champion (unseated 10-Nov-2007).

5. How these Simulations were created

All these simulations are, of course, not hand-crafted. They are generated from TM descriptions (transition table) by an "awk" program, which I wrote for this special purpose.

• The awk program for the first three simulation styles (23K) is quite experimental.
• The awk program for real macro machines (209K) is based on the above awk program, and extends it considerably.

You may use these awk programs as you like. They are given as source in order to practically demonstrate a way to implement a good TM simulator, which is capable to simulate non-trivial machines with acceptable speed, even when the underlying language is interpreted (and therefore slow). Execution times for the above simulations range from less than a second to a few minutes on a modern PC (in 2004). Altogether they need less than 10 minutes on a modern PC (in Nov-2005).

In fact, I have used the second awk program (with PA-CTRs) to run all the above machines from the 6-state record lists until they halt. The running time for #q (the former champion) was the largest: several days, due to the then really naive and therefore slow bignum implementation. With the current (Dez-2004) tuned version I did run #r in 1 hour to its halt.

I have used these awk programs with GNU "gawk", IRIX "nawk", and Solaris "nawk" (although the latter has bugs I had to work around). These awk programs should work with any (new) awk that has functions. Of course, if you find any bugs in them, please let me know.

These awk programs are not a frozen release. I will continue to develop them.

6. Change Log

• Recent changes are listed near the top.
• 27-Oct-2008: Austin Wood (a student at RMIT in Melbourne, Australia) announces independent confirmations for most 6-state 2-symbol TMs: from our new record list entries #a..#r, and from T.J. and S.Ligocki #a and #b. Communicated by email on 09-Oct and 24-Oct.
• 08-Jan-2008: Added 2 new champions communicated by email from Terry & Shawn Ligocki:

      TM type       Steps       Non-zeros         email received
      -------    -----------   -----------        -----------
       2 x 6     2.415e+9866   1.903e+4933    #g  02-Jan-2008
       4 x 3     1.025e+14072  1.383e+7036    #i  02-Jan-2008 

• 26-Dec-2007: Added 3 new champions communicated by email from Terry & Shawn Ligocki (already mid of December):

      TM type       Steps       Non-zeros         email received
      -------    -----------   -----------        -----------
       3 x 4     5.254e+13036  3.743e+6518    #i  09-Dec-2007
       4 x 3     5.318e+12068  4.210e+6034    #h  13-Dec-2007
       6 x 2     2.584e+2879   4.640e+1439    #b  13-Dec-2007 

  Again, they have improved the classical 6-state record, this time by a significant amount!
• 09-Dec-2007: Added a new champion with 4 states and 3 symbols (#g) communicated by email from Terry & Shawn Ligocki. It runs for >7.9*10⁹⁸⁶³ steps and writes >8.9*10⁴⁹³¹ non-zeros.
• 02-Dec-2007: Added a new champion with 3 states and 4 symbols (#h) communicated by email from Terry & Shawn Ligocki. It runs for >5.9*10⁴⁷⁴⁴ steps and writes >2.3*10²³⁷² non-zeros.
• 01-Dec-2007: Added a new champion with 4 states and 3 symbols (#f) communicated by email from Terry & Shawn Ligocki. It runs for >3.9*10⁹¹²² steps and writes >2.5*10⁴⁵⁶¹ non-zeros.
• 25-Nov-2007: Added 2 new champions and one good machine communicated by email from Terry & Shawn Ligocki:

      TM type       Steps      Non-zeros
      -------    -----------  -----------
       4 x 3     3.731e+1973  8.080e+986     #d
       3 x 4     3.462e+4710  1.421e+2355    #g  new champion
       2 x 6     2.568e+9863  6.940e+4931    #f  new champion 

• 24-Nov-2007: Added a new champion with 4 states and 3 symbols (#e, was named #d for 2 days) communicated by email from Terry & Shawn Ligocki. It runs for >3.9*10⁷⁷²¹ steps and writes >4.0*10³⁸⁶⁰ non-zeros.
• 10-Nov-2007: Added 6 (!) new champions communicated by email from Terry & Shawn Ligocki:

       TM type       Steps      Non-zeros
       -------    -----------  -----------
        3 x 3     1.191e+17    3.746e+8
        2 x 5     1.902e+704   1.780e+352
  
        6 x 2     8.929e+1762  2.500e+881
        4 x 3     7.785e+1618  1.610e+809
        3 x 4     8.480e+2601  1.783e+1301
        2 x 6     4.983e+1643  8.646e+821 

  Of special interest is the new 6x2 record: it is part of the classic busy beaver game and unseats the Buntrock/Marxen candidate, since 2.5*10⁸⁸¹ > 1.2*10⁸⁶⁵! [*sigh*]
• 25-Oct-2007: Added a new champion with 3 states and 4 symbols (#e) communicated by email from Terry & Shawn Ligocki. It runs for >3.1*10¹²⁵⁶ steps and writes >2.1*10⁶²⁸ non-zeros.
• 23-Oct-2007: Added a new champion with 4 states and 3 symbols (#b) communicated by email from Terry & Shawn Ligocki. It runs for >1.5*10¹⁴²⁶ steps and writes >1.1*10⁷¹³ non-zeros. That is already close to the current 6x2 champion.
• 23-Oct-2007: Added two(!) new champions with 2 states and 5 symbols (#l & #m) communicated by email from Terry & Shawn Ligocki. Both yield the exact same numbers: they runs for >1.6*10²¹¹ steps and write >5.2*10¹⁰⁵ non-zeros.
• 17-Oct-2007: Added a new champion with 2 states and 5 symbols (#k) communicated by email from Terry & Shawn Ligocki. It runs for >5.2*10⁶¹ steps and writes >9.3*10³⁰ non-zeros. Obviously, 2 states and 5 symbols is much better than 5 states and 2 symbols. Sigma(2,n) appears to be dominated by Sigma(n,2).
• 14-Oct-2007: Added a new champion with 3 states and 4 symbols (#d) communicated by email from Terry & Shawn Ligocki. It runs for >7.6*10⁸⁶⁸ steps and writes >4.6*10⁴³⁴ non-zeros.
• 05-Oct-2007: Added a new champion with 3 states and 4 symbols (#c) communicated by email from Terry & Shawn Ligocki. It runs for >4.3*10²⁸¹ steps and writes >6.0*10¹⁴⁰ non-zeros. This is a much more impressive TM, exactly as they suspected!
• 27-Sep-2007: Added a new champion with 2 states and 6 symbols (#d) communicated by email from Terry & Shawn Ligocki. It runs for >2.3*10⁵⁴ steps and writes >1.9*10²⁷ non-zeros. They comment: We suspect there are much more impressive 2x6 machines ...
• 24-Sep-2007: Added a new champion with 3 states and 4 symbols (#b) communicated by email from Terry & Shawn Ligocki. It runs for >5.7*10⁵² steps and writes >2.4*10²⁶ non-zeros. They comment: We suspect there are much more impressive 3x4 machines ...
• 22-Aug-2006: Added a new champion with 3 states and 3 symbols (#a) communicated by email from Terry & Shawn Ligocki (20-Aug-2006), boosting Sigma(3,3) to at least 95,524,079.
• 16-Aug-2006: Added 7 new champions with 2 states and 5 symbols (#d-#j) communicated by email from Terry & Shawn Ligocki. This boosts up non-zeros to 1.7*10¹¹ and the steps to even 7*10²¹!
• 26-Jul-2006: After Terry & Shawn Ligocki confirmed the results of #j from Lafitte/Papazian, I found that my own simulation software cannot complete this machine. Hence I wrote a new ML program with which today I could confirm them, too. The new program does not use fixed sized macro symbols, but rather remembers transitions for finite sized contextes around the head, growing symbol by symbol as occurring/needed. That method seems to be especially suited for counting machines: this new program needs only 9 seconds to simulate this TM. The new simulation cannot yet be seen here.
• 08-Jul-2006: Added a new step champion with 2 states and 5 symbols (#j) communicated by email from Gregory Lafitte and Christophe Papazian on 04-Jul-2006. Due to (mostly) counter like behaviour it yields only 143 non-zeros. Amazing!
• 02-Jul-2006: Added a new champion with 2 states and 5 symbols (#i) communicated by email from Gregory Lafitte and Christophe Papazian.
• 08-May-2006: Added a new champion with 2 states and 5 symbols (#h) communicated by email from Gregory Lafitte and Christophe Papazian.
• 04-Apr-2006: Added yet another record TM with 3 states and 3 symbols (#e) communicated by email from Gregory Lafitte and Christophe Papazian. This nearly doubles Sigma(3,3) to 2,950,149.
• 07-Dec-2005: Added a new record machines with 2 states and 5 symbols (#g), communicated by email from Gregory Lafitte and Christophe Papazian. It does not increase Sigma, but S, so now we have the unusual situation of two different champions for steps and non-zeros.
• 12-Nov-2005: Added 3 new (non-halting) 5-state machines with unusual symbol sizes (#u9, #u13 and #u154). They were found already long ago, but up to now I did not take the time to analyse or even publish them. Voila, here they are. The #u154 is especially noteworthy; I have no idea what's going on there. (Warning: the PA-CTR version of #u154 is large, ca 1MB!)
• 23-Oct-2005: Added two new record machines with 2 states and 5 symbols (#e, #f), communicated by email from Gregory Lafitte and Christophe Papazian. Sigma(2,5) now is at least 1,957,771... much larger then the 4098 known for Sigma(5,2).
• 4-Oct-2005: Added the new record machine with 2 states and 5 symbols (#d), communicated by email from Gregory Lafitte and Christophe Papazian.
• 10-Sep-2005: Added yet another record TM with 3 states and 3 symbols (#d) communicated by email from Gregory Lafitte and Christophe Papazian. This boosts Sigma(3,3) from the former 107900 to amazing 1525688, and S(3,3) to 987'522'842'126. Wow!
• 4-Sep-2005: Added 2 new record machines with 2 states and 5 symbols, communicated by email from Gregory Lafitte and Christophe Papazian on 17-Aug-2005, and yet another one from 4-Sep-2005.
• 9-Aug-2005: Added 2 new record machines with 3 states and 3 symbols, communicated by email from Gregory Lafitte and Christophe Papazian. Both TM surpass the former champions from Myron Souris.
• 18-Jul-2005: Added 2 new record machines with 3 states and 3 symbols, communicated by email from Myron Souris, who found them in 1995, already, but "didn't think anyone would be interested" ;-)
• 01-May-2005: Added 4 new machines with 2 states and 5 and 6 symbols, with 3 states and 4 symbols, and with 4 states and 3 symbols from Terry J. Ligocki and Shawn Ligocki, all of which are new champions (in there respective category).
• 16-Feb-2005: Added 5 new machines with 2 states and 4, 5 and 6 symbols from Terry J. Ligocki and Shawn Ligocki, all of which are new champions (in there respective category).
• 09-Jan-2005: Added PPA-CTRs, connecting the gaps between PA-CTRs. Some TMs gain significantly, but some do not gain much. From the 6-state record list the following now are shown to halt: #d, #i, #j and #k.
• 09-Jan-2005: Shortened some excessively long numbers by replacing the middle part by an indication of the omitted length.
• 24-Dec-2004: The bignum simulation is significantly faster. Added some minor features.
• 11-Dec-2004: The macro machine simulations document the original input to the "awk" program.
• 06-Dec-2004: Added yet another new 3x3 champion (#c) from Allen Brady.
• 27-Nov-2004: Added 2 machines from Allen Brady with 3 states and 3 symbols (!).